- der komplette Quellcode inkl. Binärdateien für linux-x64 and win32
→ ist verfügbar auf Github - → live Demo
Motivation
Der Versuch, zumindest einfache echtzeit 3D Grafik auf Webseiten anzubieten, war immer mit Schmerzen verbunden. Bevor WebGL letztendlich von Microsoft und Apple übernommen wurde, gab es einige Technologien, die sich darum bemühten, der quasi de facto Standard für 3D Grafik im Internet zu werden.
Unwillig alle zu unterstützen, stellte ich mir die Frage:
Was, wenn ich überhaupt keine Rendering Technologie verwende?
Offensichtlich muss ich dann das komplette Rendering selbst machen.
Das klingt nach einer Herausforderung? Nun, das hängt davon ab, was du vor hast. Wenn es nur um eine triviale Projektion, eine einfache Lichtquelle und rudimentäre Texturen geht - ist das nicht so schwer, wie man annehmen würde.
Da ich 3D Grafik unter der Verwendung von OpenGL2.1 gelernt habe, konnte ich mich nie wirklich an die “neue” frei programmierbare Pipeline im heutigen OpenGL / WebGL gewöhnen. Mir gefiel die Definition von frei darin nicht, denn es ist handelt sich nicht um frei wie in du darfst das machen, tatsächlich handelt es sich um ein du musst das machen!
Obwohl ich inzwischen einigen OpenGL4.0 Code geschrieben habe, waren meine Shader zusammenkopierte Einzeiler.
Dies vorweg gesagt, habe ich aus zwei Gründen an diesem Projekt gearbeitet:
- um endlich zu verstehen, was Shader sind und was man durch ihre Nutzung erreichen kann
- um herauszufinden, ob die Leistung möglicherweise ausreicht, um als Notfallalternative genutzt werden zu können, wenn kein WebGL verfügbar ist.
Nur um das klarzustellen: Mir ist bekannt, dass es 3D rendering unterstützung in Flash und Miscrosofts Silverlight gibt. Ich halte diese Technologien lediglich für ungeeignet die heutigen Anforderungen des Internets zu erfüllen – insbesondere, wenn man auf Portabilität hin arbeitet und nicht das Selbe mit mehreren verschiedenen proprietären Technologien bauen will.
Prerequisite
Was man benötigt, um mit dem Rendern zu beginnen, ist exakt das selbe, was man für hardwarebeschleunigtes Rendern benötigen würde – dennoch würde ich es hier gerne kurz auflisten.
- ein vertex model der Objekte die man rendern möchte
- Texturemapping Koordinaten
- Normal Vektoren für Dreiecke
ein vertex model der Objekte die man rendern möchte
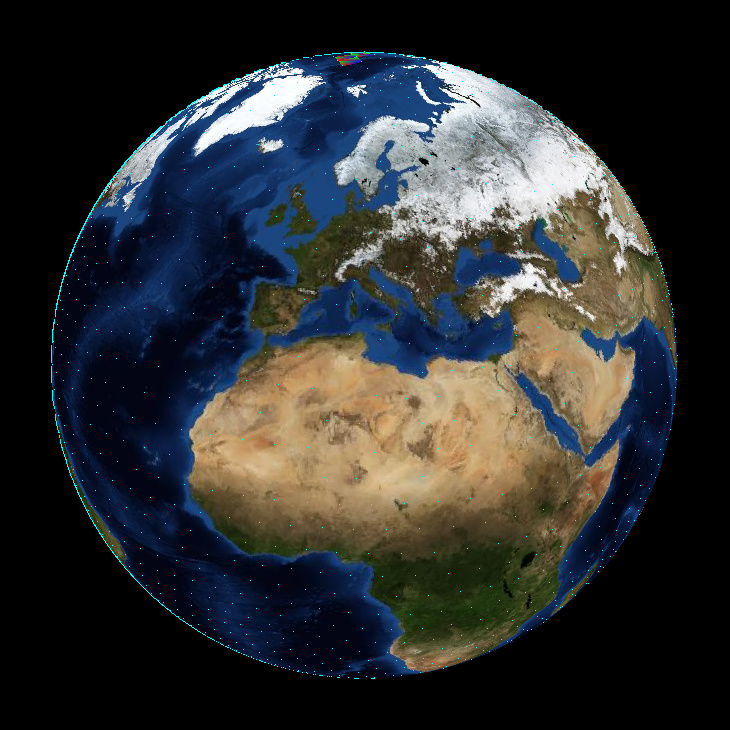
Da ich einen Globus rendern wollte, war dies ziemlich einfach. Alles was ich benötigte, war ein 5120 seitiger Ikosaeder. Das ist eine ziemlich hohe Anzahl von Dreiecken für ein Objekt, welches nur durch Software gerendert werden soll. Aber die nächst kleinere Anzahl von Dreiecken, die mathematisch möglich gewesen wäre, hätte nur 1280 davon gehabt, was schon eher wie etwas aussah, was man bei einem Tabletop Spiel rollen würde, als wie eine Kugel. Obwohl das Texturemapping dadurch ein wenig komplizierter wird, bevorzuge ich die Form des Ikosaeders gegenüber der üblichen Annäherung einer Kugel, da alle seine Seiten gleich groß sind.
Die Wireframe Ansicht eine normalen Kugelapproximation wirkt unausgewogen auf mich. Ihre Seiten werden unendlich klein an den Polen.
Ich bin mir sicher, dass es eine verblüffend einfache Formel gibt, um meinen Ikosaeder im Code zu berechnen, aber ich habe nur einige regex Ersetzungen auf ein Modell angewendet, welches ich als Wavefront .obj in Blender exportiert hatte. Da ich absolut keine Ahnung davon habe, wie man eine Weltkarte auf einen Ikosaeder überträgt, musste ich mich ohnehin auf Blender verlassen.
Texturemapping Koordinaten
Wie ich schon zuvor anmerkte, ist dies schwarze Magie für mich. Um eine Textur auf irgend etwas anderes als ein Rechteck abzubilden, benötigt man eine Abbildung der Dreiecke seines Objekts auf die Teile der Textur, die sie auffüllen sollen.

Es scheint so, als gäbe es keine perfekte Lösung für eine auf einem Ikosaeder basierte Kugel. Einfach auf UV unwrap zu klicken war ausreichend für mein Projekt.
Wie man sieht, ist auch ein Ikosaeder kein optimales Objekt für die Abbildung einer Textur auf eine Kugel. Ich bezweifle, dass es eins gibt.
Solange man eine rechtwinklige Fläche auf eine Kugel abbilden will, werden das obere und untere Ende der Textur auf die Pole abgebildet, wodurch der gesamte Bereich auf lediglich ein paar Dreiecke projiziert wird.
Erstaunlicherweise generierte Blender einige Texturkoordinaten, welche größer als eins waren. Diese sollten sich normalerweise um die Textur herumwickeln. Ich habe mich jedoch dazu entschieden, sie zu ignorieren, da es einige extra “if”s für jeden einzelnen Pixel, der gerendert werden sollte, bedeuten würde und ich nicht erwartete, dass meine Herangehensweise dafür schnell genug sei (letztendlich lag ich damit richtig).
Normal Vektoren für Dreiecke
Erneut kann man normal Vektoren einfach im eigenen Code berechnen (Kreuzprodukt), aber solange die Objekte eine statische Form haben, die nur durch die Modelview Matrix (dazu komme ich noch) modifiziert werden, braucht man das nicht.
Normal Vektoren sind praktisch für einige Dinge. Sie helfen einem, um heraus zu finden, ob ein Dreieck nach innen, oder nach außen weist, sie werden für Lichtberechnungen benötigt und sie helfen dabei, Dreiecke welche nicht aus der Kameraperspektive gesehen werden können, da sie in die Gegenrichtung weisen, zu finden.
Dies (Backface Culling) ist die einzige Technologie, für die ich normal Vektoren verwendet habe. CPU basiertes Texturmapping ist ein sehr aufwendiger Prozess, weshalb jedes Dreieck welches man nicht zeichnen muss, dabei hilft, das Rendern zu beschleunigen.
Natürlich lässt sich das nur auf nichttransparente Objekte anwenden. Andererseits könnten und sollten auch von der Kamera weg orientierte Dreiecke gesehen werden.
Bis auf die Textur konnte ich alles von Blender bekommen, wodurch ich bereit war, in den Rendering Prozess ein zu tauchen.
ToDo:
- Vertices vom 3D Objektraum zu 2D Bildschirmkoordinaten projizieren
- unsichtbare Dreiecke entfernen
- berechnen welche Bildpunkte sich wirklich in einem Dreieck befinden
- Texturpixel auf Dreiecke abbilden
All diese Schritte werden normalerweise durch die Hardware ausgeführt. Zumindest für Schritt zwei bis vier sind wir es mehr oder weniger gewöhnt, dass die Hardware sich wie eine Blackbox verhält.
Ich bin davon keine Ausnahme, so dass ich keine Ahnung davon hatte, wie dies zu tun sei, aber beginnen wir am Anfang.
Vertices vom 3D Objektraum zu 2D Bildschirmkoordinaten projizieren
Es ist egal, ob man die Hardwarebeschleunigung verwenden will, oder nicht, man muss dennoch einige Matrizen erstellen, um seine Vertices zu projizieren.
Nun… das stimmt nicht zu 100%. Tatsächlich kann man seine Vektoralgebra auch komplett ohne die Verwendung von Matrizen berechnen, aber dadurch wird der Prozess kein Stück schneller.
Also habe ich die selben Matrizen verwenden, welche ich auch für WebGL genutzt hätte.
Es erhöht die Leistung beträchtlich, wenn man die Matrizen zuvor miteinander multipliziert (zumindest für alle Vertices, auf die die selben Transformationen angewendet werden sollen):
combined = VPcorr * projection * camera * model
Von Rechts nach Links erklärt:
model: repräsentiert alle Transformationen, welche nur auf ein einzelnes Objekt, oder nur einen Teil davon angewendet werden sollen. (typischerweise Rotation, Translation und Skalierung).
camera: wenn sich die Kamera bewegt, sollte man diese Matrix verschieben und rotieren. Dies hält die Kamera von allem anderen unabhängig. Wenn du nerdig bist, kannst du stattdessen die entgegengerichtete Transformation auf alle Objekte außer der Kamera anwenden.
Wenn also die Kamera drei Schritte vorwärts in irgendeine Richtung macht, kann man genauso die ganze Welt in die entgegengesetzte Richtung verschieben.
Die Kamera Matrix ist also nur ein Konstrukt zur Bequemlichkeit.
projection: Dies ist der Ort, wo es magisch zugeht. Ich werde mich nicht über Details auslassen. Falls jemand daran interessiert ist, sollte er die entsprechenden Absätze in der OpenGL Dokumentation lesen. Dort habe ich gelernt wie man diese Matrix Komponente für Komponente aufbaut.
Will man eine orthographische Projektion erreichen, gibt es nicht viel mehr als Skalierung und Verschiebung in dieser Matrix.
Will man hingegen wie ich eine perspektivische Projektion, wird es ein Stück komplizierter, aber erneut verschone ich dich mit den Details.
Ein letztes Detail gibt es noch zu erwähnen: Wenn man nicht die hardwarebeschleunigte Rendering Pipeline verwendet, muss man jede x und y Koordinate durch die dazugehörige z Koordinate teilen. Die Hardware tut dies implizit. Vergisst man das also, wird die Projektion eher wie eine fehlerbehaftete orthographische Projektion aussehen.
Was ist mit VPcorr?
Ich bin froh, dass dir das aufgefallen ist. Jetzt wo du danach fragst: Dies ist eine weitere Berechnung, die man nicht machen müsste, wenn man Hardware Rendering verwendet, da die Hardware die virtuelle Projektion automatisch in Bildschirmkoordinaten einpasst.
Die Koordinaten, die man aus der Projektion erhält, befinden sich immer noch zwischen minus Eins und Eins. Offensichtlich ist das nicht sehr nützlich, um Pixel auf eine Zeichenfläche zu bringen, deren Koordinaten immer positiv sind und die ihren Ursprung bei Null/Null in der Ecke hat.
VPcorr skaliert das Koordinatensystem um die hälfte der Zeichenflächengröße in jede Richtung und verschiebt den Ursprung in die Mitte der Zeichenfläche.
Von diesem Punkt an können wir diese Koordinaten direkt als Koordinaten auf der Zeichenfläche benutzen. Es gibt zwar immer noch eine z Koordinatem, welche wir später noch benutzen werden, aber für den Arbeitsschritt Zeichenflächenkoordinaten zu bekommen, brauchen wir diese nicht mehr.
Jetzt wo wir eine kombinierte Matrix haben, was machen wir damit?
Der hardwarebeschleunigte Fall: Man hätte die Matrizen nicht einmal multiplizieren müssen – stattdessen reicht es, sie an einen Vertex Shader zu übergeben, welcher die Berechnungen für uns macht.
Wenn man wirklich alles selbst macht: Multipliziere jeden einzelnen Vertex des Modells mit der kombinierten Matrix, speichere sie zwischen und vergiss nicht am Ende durch die z Koordinate zu teilen.
Das Resultat im Speicher entspricht den Vertices projiziert auf die Zeichenfläche für ein Einzelbild.
Wenn sich das Objekt bewegt, muss man offensichtlich alles für das nächste Einzelbild wiederholen, aber das ist noch nicht der Teil, der die CPU aufheizt.
Unsichtbare Dreiecke entfernen
Da die Geschwindigkeit des Renderns großteils davon abhängt, wie viele Dreiecke man rendern will, ist es immer eine gute Idee, jene zu entfernen, die anderenfalls durch Dreiecke überzeichnet würden, die sich näher an der Kamera befinden.
Solange man nicht mit Transparenzen arbeitet, ist die simpelste Technik, die man implementieren kann Backface Culling. Alles, was man dazu tun muss ist dies:
- Modelview- und Projektionsmatrix auf die normal Vektoren anwenden
- das Skalarprodukt zwischen den normal Vektoren und der Kamera berechnen
- alle Dreiecke für welche das Ergebnis größer als Null ist verwerfen, denn es repräsentiert einen Winkel von über 90°, was man als von der Kamera abgewandt interprätieren kann
Das klingt einfach? Ich muss zugeben, irgendwie habe ich das verbockt. Das zusätzliche Anwenden der Projektionsmatrix führte zu seltsamen Ergebnissen, so dass ich nur die Modelviewmatrix verwendet habe, bevor ich das Skalarprodukt gebildet habe.
Das ist inakkurat, da eine perspektivische Projektion die normal Vektoren ebenfalls verändert. In meinem Fall blieben mehr abgewandte Dreiecke zurück, als meine Backface Culling Implementierung finden konnte.
Wenn dein Backface Culling nicht gut ist, oder du mit Transparenzen arbeitest, oder du mit Objekten arbeitest, die komplexer sind als geometrische Standartobjekte wie Kugeln, oder Würfel – kurz gesagt: immer – dann gibt es da noch eine Sache die du tun solltest:
Alle Dreiecke müssen nach ihrer Position auf der z Achse sortiert werden.
Wann man das nicht macht und einfach alle Dreiecke in der Reihenfolge zeichnet, wie sie sich im Puffer befinden, dann wird man Dreiecke, die weiter weg von der Kamera sind, über solche zeichnen, die näher dran sind. Falls du etwas empfindlich bis, könnte dies dazu führen, dass du dich übergeben musst - dein Gehirn hat nie etwas derartiges gesehen (das ist mein Ernst).
Ich habe einfach QSort mit einer Callbackfunktion verwendet, die z Koordinaten vergleicht.
Ich bitte darum, das jetzt nicht falsch zu verstehen: Die Dreiecke nach ihrer z Koordinate zu sortieren, entfernt natürlich keine weiteren Dreiecke, welche nicht gezeichnet werden müssten. Es schützt nur davor, sie zum falschen Zeitpunkt zu zeichnen.
Sie sind immern noch da, aber man kann damit sicher stellen, dass Dreiecke die näher an der Kamera sind, darüber gezeichnet werden.
Zumindest ist das Resultat auf dem Bildschirm jetzt korrekt.
berechnen, welche Bildpunkte sich wirklich in einem Dreieck befinden
Das Grab für die Rechenleistung liegt hier. Über dieses Problem habe ich nie richtig nachgedacht, obwohl ich dazu irgendwas an der Uni gelesen haben muss. Ich hatte nicht das Bedürfnis in alten Papieren zu wühlen, also habe ich versucht diese Nuss mit meinem eigenen Kopf zu knacken.
Lasst uns damit beginnen eine minimale, rechteckige Fläche zu definieren, die das Dreieck enthält.
Die bekommt man, indem man die minimalen und maximalen x und y Koordinaten des Dreiecks bestimmt. Sie definieren zwei Ecken des Rechtecks, was ausreicht, um über alle Pixel zu iterieren.
Um das Dreick zu zeichnen, muss man für jeden Pixel des Rechtecks überprüfen, ob er sich innerhalb, oder außerhalb des Dreiecks befindet. Aber wie überprüft man das?
Der triviale Ansatz ist es, alle drei Vertices an den Ecken zu nehmen und sie zu Vektoren konvertieren, indem man sie voneinander subtrahiert.
(Mögen sie A, B, C genannt werden.)
v1 = A - B v2 = B - C v3 = C - A
Diese Vektoren rotieren (mathematisch gesehen Unfug) um das Zentrum des Dreiecks. Gab es da nicht eine Formel, um zu überprüfen, auf welcher Seite einer Grade sich ein Punkt befindet?
Gegeben eben diese, müsste ein Punkt, welcher sich auf der gleichen (richtigen) Seite aller drei Graden befindet, im Dreieck liegen. Die relevante Seite hängt davon ab, wie rum die Vektoren um das Zentrum weisen und welche Seite es dann ist.
Auf der Suche nach einem Codeschnipsel, den ich anpassen könnte, stolperte ich über eine Seite, die eine viel bessere Lösung erklärte (englisch).
Der Author empfiehlt stattdessen eine Koordinatensystemtransformation durchzuführen, wodurch man weniger Instruktionen benötigt.
Nimmt man einen Vektor als Ursprung und die Subtraktion des Ursprung von den übrigen beiden als Einheitsvektor, erhält man ein frisches neues Koordinatensystem. Dieses Koordinatensystem ist nur für den Sonderfall kartesisch, dass der Winkel zwischen den beiden Einheitsvektoren 90° betrug, aber das ist für die weitere Verwendung egal.
Man kann immer noch jeden Punkt in diesem Koordinatensystem durch eine Linearkombination der beiden Einheitsvektoren beschreiben.
Streng genommen ist dies die Definition eines Koordinatensystems.
In Pseudocode sieht das dann so aus:
P = u * v1 + v * v2
Wobei P ein Punkt ist, u & v beliebige Faktoren und v1 & v2 die Einheitsvektoren.
Das Schöne daran ist, dass man beweisen kann, das jeder der Punkte innerhalb des Dreiecks die folgenden Bedingungen erfüllen muss:
(u >= 0) && (v >= 0) && (u + v < 1)
Um P zu erhalten, muss man lediglich den neuen Ursprung wieder subtrahieren, u & v zu erhalten ist etwas komplizierter, aber es ist immer noch weniger aufwändig (gemessen in Instruktionen), zu testen, ob ein Punkt Teil eines gefüllten Dreiecks ist.
Wenn es dich interessiert, solltest du die original Seite lesen (englisch).
Wissend, welche Pixel zu einem Dreieck gehören, könnte man es mit einer konstanten Farbe füllen. Aber was ist mit Texturen?
Lies weiter!
Texturpixel auf Dreiecke abbilden
Wieder einmal hatte ich Anfangs keine Ahnung wie man das anstellen sollte. Dass heist, bevor ich die Faktoren u & v aus dem letzten Schritt hatte. Die abgebildeten Dreiecke auf der Textur mögen zwar total verzerrt, gedreht und … in anderen Worten, verschwurbelt aussehen, aber was für die Dreiecke in Bildschirmkoordinaten gilt, ist ebenfalls gültig für die abgebildeten Dreiecke.
Wenn man sie zu einem Ursprung und zwei Einheitsvektoren konvertiert, wie ich es bereits zuvor gemacht habe, kann man genau die gleichen Faktoren u & v benutzen und eine Linearkombination der Einheitsvektoren und Faktoren bilden.
Das ist wirklich alles was man benötigt, um den passenden Texturpixel für einen Bildschirmpixel zu erhalten. Der Texturpixel ist zwar immer noch relativ zum berechneten Ursprung, aber das kann man beheben, indem man den Vektor zurück addiert, den wir zuvor subtrahiert hatten, um den neuen Ursprung zu erhalten.
Mit diesem Wissen, sollte es recht einleuchtend sein, dass der Test, ob sich Pixel in einem Dreieck befinden und das übertragen einer Farbe aus der Textur, in der selben Schleife erledigt werden sollte.
Was ist mit Licht?
Ja, das stimmt natürlich. Alle meine Pixel, die auf diese Art abgebildet wurden, haben die volle Intensität der Textur. Um es kurz zu halten, Licht und Reflexionen sind Berechnungen mit den normal Verktoren der Dreiecke, einem Vektor, der auf die Lichtquelle(n) zeigt und einem Vektor in Richtung der Kamera. Man muss Winkel berechnen, sie gewichten, addieren und das Ergebnis mit der Farbe der Textur multiplizieren und kann so alle möglichen virtuellen Lichteindrücke erreichen.
Eine virtuelle Sonne zu haben, wäre sicherlich interessant gewesen, aber mein Code ist bereits langsam genug… .
Das sieht jetzt aber nicht gerade wie heutige Computerspiele aus. Könnte man Anti-Aliasing hinzufügen?
Natürlich kann man das. Es ist sogar einfach. Aber zur gleichen Zeit würde die Zeit zur Berechnung explodieren. Ich gebe mal einen Hinweis, wie man das generell anstellen würde.
Man würde nicht testen, ob ein Pixel Teil eines Dreiecks ist, sondern, ob ein Subpixel es ist. Anstatt einen rechteckigen Bereich um das Dreieck Pixel für Pixel abzusuchen, würde man nur einen halben Pixel, einen viertel … und so weiter. Da dies ein zweidimensionales Koordinatensystem ist, würde die Berechnungszeit quadratisch steigen.
Um eine bessere Texturqualität zu erhalten, würde man zum Beispiel nicht nur einen einzelnen Pixel kopieren, sondern eine n-Pixel Umgebung mit einem gewichteten Gausskern abtasten.
Dies wiederum wäre eine furchtbare Sache, um sie auf der CPU zu berechnen.